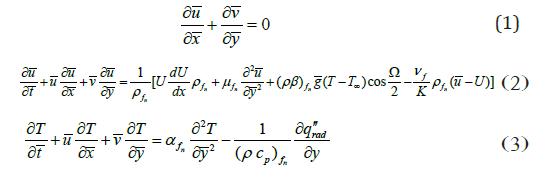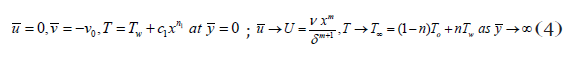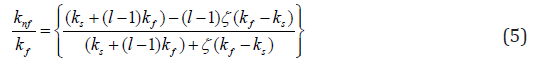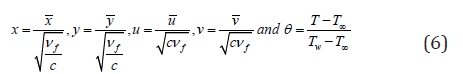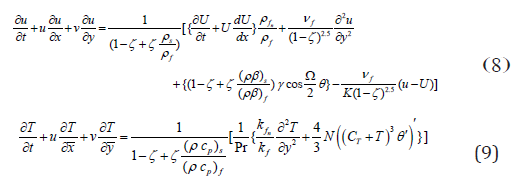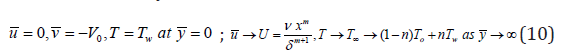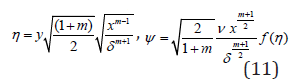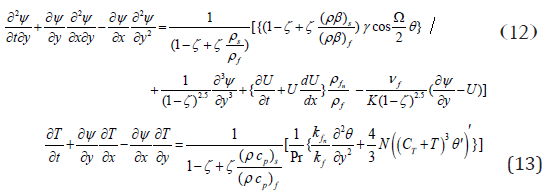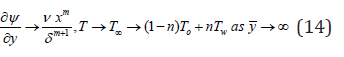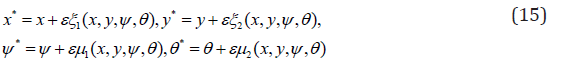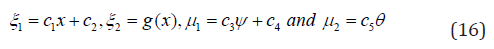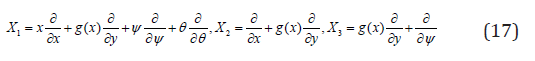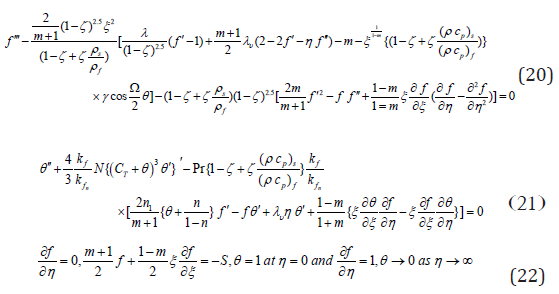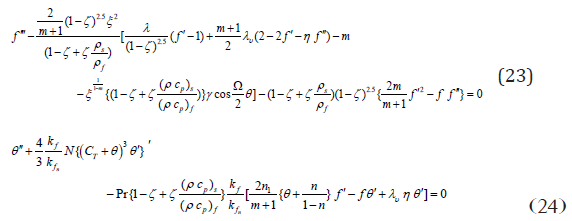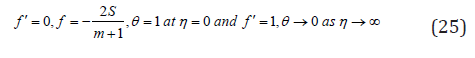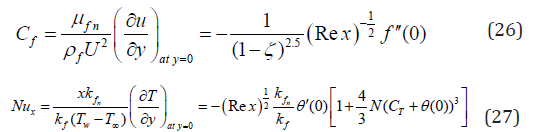Solar Radiation Energy Issues on Nanoparticle Shapes in the Potentiality of Water Based Cu, Al2O3 and SWCNTs Volume 1 - Issue 2

R Kandasamy*, Mohammed Mahdi Fayyadh and Radiah Mohammad

• Research Centre for Computational Fluid Dynamics, FSTPI, Universiti Tun Hussein Onn Malaysia, Malaysia

Received: May 13, 2018;   Published: May 24, 2018

*Corresponding author: R Kandasamy, Research Centre for Computational Fluid Dynamics, FSTPI, Universiti Tun Hussein Onn Malaysia, Malaysia

DOI: 10.32474/ANOAJ.2018.01.000110

Abstract PDF

---

Abstract

Energy is an extensive view for industrial advancement. Solar thermal energy is designed by light and heat which is radiated by the sun, in the form of electromagnetic radiation. Solar energy is the highest promptly and sufficiently applicable authority of green energy. Impact of nanoparticle shapes on the Hiemenz nano fluid (water based Cu, Al2O3 and SWCNTs) flow over a porous wedge surface in view of solar radiation energy has been analyzed. The three classical form of nanoparticle shapes are registered into report, i.e. sphere , cylinder and laminar . Nanoparticles in the water based Cu, Al2O3 and SWCNTs have been advanced as a means to boost solar collector energy through explicit absorption of the entering solar energy. The controlling partial differential equations (PDEs) are remodeled into ordinary differential equations (ODEs) by applying dependable accordance alteration and it is determined numerically by executing Runge Kutta Fehlberg method with shooting technique. It is anticipated that the lamina shape SWCNTs have dynamic heat transfer attainments in the flow improvement over a porous wedge surface as compared with the other nanoparticle shapes in different nano fluid flow regime.

Keywords: Nano Particle Shapes, Unsteady Hiemenz Flow, Water Based Cu, Al2O3 and Swcnts, Solar Energy Radiation, Nano Fluids, Solar Thermal Energy, Progressive Technology, Volumetric Receivers, Thermal Attitude

Introduction

Recently nano fluid (water based Cu, Al2O3 and SWCNTs) attracts a noticeable application due to its remarkably energetic heat transfer mechanism. Solar thermal energy is an ideal significant in our regular benefit and it’s a usual system of accessing heat, electricity and water with assist from the nature. As we will address some fossil fuels situation, the solar thermal energy is a sustainable expert of energy which never exhausts. Sustainable energy generation is one of the most important challenges facing society today. Solar thermal energy is one of the principal experts of renewable energy with basic coincidental impact, Sharma et al. [1]. The essential view of ANOAJpting particles to assemble solar energy was analyzed in the 1970s by Hunt [2]. Nanoparticles attempt the possible of developing the radiative assets of liquids, outstanding to enhance in the capability of explicit absorption solar collectors. Heat transfer in the nano fluids (water based Cu, Al2O3 and SWCNTs) due to solar radiation energy is of considerable practical influence to engineers and scientists as a result of its relatively global event in countless units of science and engineering, Choi [3], Buongiorno and Hu [4], Buongiorno [5] and Cheng and Minkowycz [6]. Once again, science and progressive technology is much obliged to solar radiation due to its extensive utilization in the design of solar thermal electricity, solar photovoltaic cells, solar heating, artificial photosynthesis, etc.

Nanoparticle shapes (sphere, cylinder and lamina) in the nano fluids (water based Cu, Al2O3 and SWCNTs) absorb solar radiation notably because of small size as correlated to the wavelength of de Broglie wave. Therefore nanoparticles also attempt the assuring aspect of strengthening the radiative resources of liquids, dominating to accelerate in the performance of straight absorption of solar collectors, [7,8]. Recently, the effects of solar radiation on nano fluid with variable stream conditions were addressed by Das et al. [9] and Anbuchezhian et al. [10].

Many investigators [11-16] have analyzed the utilization of these new transport of heat transfer in solar collectors. Yousefi et al. [11] experimentally presented that the Al2O3/water nanofluid increases the ability of flat-plate collectors by 28.3%. Yousefi et al. [12] studied the effects of pH values of carbon nanotubes nanofluids on the expertise of a flat-plate solar collector. Kameya and Hanamura [13] addressed that the radiation absorption resources of base fluid were increased harmfully by including Ni nanoparticles. Lenert and Wang [14] analyzed the efficiency of nanofluids as volumetric receivers in concentrated solar utilizations applying the suspension of carbon-coated cobalt nanoparticles into Therminol VP-1 fluid. He et al. [15] practically addressed the applicable photo-thermal assets of Cu/H2O nanofluids for enrollment in blunt absorption, solar thermal energy systems.

Furthermore, the up-to-date revision papers [17,18] recorded that nanofluids have strong accessible for utilizations in solar organizations such as solar collectors [19], photovoltaic thermal schemes [20], and thermal energy storage structures [21]. Most of the analysis on the employment of nanofluids in solar collectors has been defined to energy and energy investigations. There are some analyzes on the investigation of the hydrodynamic and convective heat transfer assets of nanofluids in solar structures [16]. As displayed in many review articles [22-24], a massive amount of practical work has been addressed on the thermal attitude of various types of nanofluids flowing through different heat exchanger models; among them, the circular successive tubes have admitted more application in this study since they are the main elemental of various types of solar collectors.

Recently, the capability of applying both nanofluid and porous media has admitted comfortable absorption and has attended to broad analysis in this field. Porous media enhance the association surface area among liquid and solid surface, and, on the other hand, nanoparticles circulated in nanofluid upgrade the impressive thermal conductivity. Therefore, it suggests that utilizing both porous media and nanofluid can enhance the ability of typical thermal systems harmfully. Convective flow in porous media has been universally analyzed in the recent years due to its extensive operations in engineering as post-accidental heat dismissal in solar heater or collectors, drying generating processes, heat exchangers system, geothermal and oil recovery scheme, building construction region, etc. Heat and mass transfer for Hiemenz flow through porous media in the presence of an incident external magnetic field have been studied by several authors [25-30].

The method of Lie group transformations is used to derive all group-invariant similarity solutions of the unsteady twodimensional laminar boundary layer equations, Yurusoy and Pakdemirli [18], Yurusoy and Pakdemirli [19] and Avramenko et al. [31]. Impact of thermal stratification is an important aspect in heat transfer analyses. Thermal stratification of nanofluids occurs due to temperature variations or the presence of different fluids of different densities.

In this article, we addressed the role of nanoparticle shapes (sphere, cylinder and lamina) in the presence of unsteady nanofluids (water based Cu, Al2O3 and SWCNTs) flow and heat transfer past a porous wedge sheet due to solar radiation. Lie symmetry group transformation is applied to transform the controlling PDEs into ODEs and then the numerical solution of the problem is cultivated by using fourth or fifth order Runge Kutta Fehlberg method with shooting technique. Experimental works have analyzed that the nanoparticle shape has a unique impact on the heat and mass transfer of nanofluids [32,33]. Nanoparticle shapes i.e. sphere, cylinder and laminar, are authorized into address in this work. The parameter affirmation for the problem was accomplished and is authorized. It is consumed that the results will gift towards better understanding of nanofluid conflict in channel. Several aspects of the problem are analyzed and predicted graphically with account to the physical parameters elaborated within it and the instant improvements are associated with the applicable literature.

Mathematical Analysis

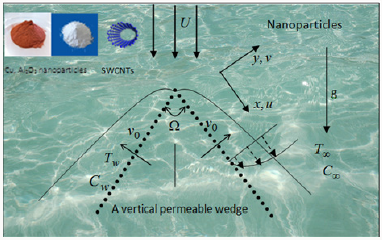
Consider the unsteady laminar two-dimensional flow of an incompressible viscous nanofluids (water based Cu, Al2O3 and SWCNTs) past a porous wedge sheet in the presence of solar energy radiation (Figure 1). The porous medium is assumed to be transparent and in thermal equilibrium with the fluid and neglecting the pressure gradient in the y direction. Due to heating of the entrancing nanofluid and the wedge surface by solar thermal radiation, heat is transmitted from the plate. Also, the solar radiation is a collimated beam that is normal to the plate. The working water based Cu, Al2O3 and SWCNTs nanofluid flow is assigned to be Newtonian. The system of regulating equations are designated are

Employing Rosseland approximation for thermal radiation Sparrow and Cess [34], Rapits [35] and Brewster [36], q_radⁿ=-4σ₁/3k* ∂T⁴/∂y, σ₁- the Stefan-Boltzman constant, k* - the mean absorption coefficient. The Rosseland relation is recycled to define the thermal radiative heat transfer in the restraint of the optically thick fluid (nanofluid).

With boundary conditions

(Power index) are constants and V₀ and T_w are (the suction ( V₀ > 0 ) or injection ( V₀ < 0 )) velocity and the fluid temperature at the plate. The feasible flow velocity of the wedge is U_(x,t)=v x^m/δ^m+1,β₁=2m/1+m Sattar [37] whereas δ is the time-dependent length scale, δ =δ (t) and the Hartree pressure gradient parameter, β₁=Ω/π,Ω - angle of the wedge, the temperature of the fluid is simulated to differ succeeding a power-law function while the free stream temperature is linearly stratified. In equation (4) and n is a constant parameter assigned as the thermal stratification parameter, 0 ≤ n <1. T₀ =T_∞ (0) is a constant reference temperature. The suffixes w and ∞ denote surface and ambient conditions. Let u and v are the velocity components along the x and y directions, T - the local temperature of the nanofluid, g - the acceleration due to gravity, K - the permeability of the porous medium, ρ f_n- the effective density of the nanofluid, rad q′′ - the applied absorption radiation heat transfer, μ f_n - the effective dynamic viscosity of the nanofluid, α f_n - the thermal diffusivity of the nanofluid, Aminossadati and Ghasemi [38] which are defined aρ_s =(1 −ζ)ρ_f+ζρ_s, μ_fn=μ_f/(1 − ζ )^2.5,,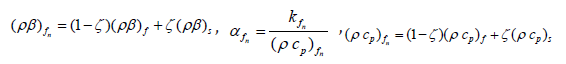

Maxwell model [39] was refined to define the effective electrical or thermal conductivity of liquid-solid suspensions. Let k_f and k_s - the thermal conductivity of the base fluid and nanoparticle, ζ - the nanoparticle volume fraction, μ_f - the dynamic viscosity of the base fluid, β_f and β_s - the thermal expansion coefficients of the base fluid and nanoparticle, f ρ and ρ_s - the density of the base fluid and nanoparticle, k_fn - the effective thermal conductivity of the nanofluid and (ρ c_p)f_n- the heat capacitance of the nanofluid.

Proposing the succeeding non-dimensional variables

Based on the above results, the equations (1) - (4) become

∂u/∂x+∂v/∂y=0 (7)

With boundary conditions

Pr= ν_f/α_f- the Prandtl number,λ=δ^m+1/ K k²- the porous media paramet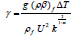er, - the buoyancy or natural convection parameter,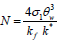- the conductive radiation parameter, where θ_w=1/T_w-T_∞≅0.1.Let γ > 0 aids the flow and γ < 0 opposes the flow, while γ = 0 i.e.( ) w T T∞ − , represents the case of forced convection flow. Hence, combined convective flow exists when γ = O(1). Based on Kafoussias and Nanousis [20]

and θ=T-T_∞/T_w-T_∞,u=∂ψ/∂y and v=-∂ψ/∂x

The system of equations (7) - (9) become

With the boundary conditions

∂ψ/∂y=0,∂ψ/∂x=-V₀,T=T_w at y=0,

where C_T=T_∞/T_w-T_∞ - the temperature ratio, 0.1 T C = and heat radiation 0 ≤ N ≤1.0 , Murthy et al. [40].

The symmetry groups of Equs. (12) and (13) are estimated applying the classical Lie group approach as

It is noted that the form of infinitesimals as

g(x) - An arbitrary function.

Definitions of infinitesimal alternators are

The PDEs controlling the work under attention are converted by a exclusive mode of Lie symmetry group conversions viz. oneparameter infinitesimal Lie group of transformation into a system of ODEs. For the current situation, we considered that the generator 1 X with g(x) = 0 . The distinctive equations are

dx/x=dy/0=dψ/ψ=dθ/θ (18)

Based on the above equations, it is calculated as

η = y,ψ = x f(η ) and θ = xθ (η ) Where η =η (x,t) (19)

Established on these relations, the Equs. (12) and (13) become

S - The suction parameter if S > 0 and injection if S < 0 and

ξ =k x^1-m/2 the dimensionless distance along the wedge (ξ > 0 ) [41].In this scheme of equations, it is predicted that the non similarity forms of the problem are exhibited in the terms involving partial derivatives with respect to ξ . Generation of the local nonsimilarity schemes with reference to the current work will now be reviewed. At the first level of truncation, the terms followed by ξ ∂/∂_ξ are small. This is notably true when (ξ <<1). Therefore the terms with ξ ∂/∂_ξ on the right-hand sides of Equations (20) and (21) are eliminated to obtain the succeeding scheme of equations:

With boundary conditions

Suppose that λ_υ= c/x^m1, = , c is a constant so that c=δ^m/v ∂δ/∂t and integrating, it is predicted that δ = [c(m+1)ν t]^{1/ m+1} . In spite of c = 2 and m =1 in δ and we obtain δ = 2 ν t which observes that the parameter δ can be correlated with the well settled scaling parameter for the unsteady boundary layer problems [42].

For experimental principles, the functions f (η ) and θ (η ) grant us to define the skin friction coefficient and the Nusselt number as

Here, Re_x=U x/v _f = is the local Reynolds number.

Results and Discussion

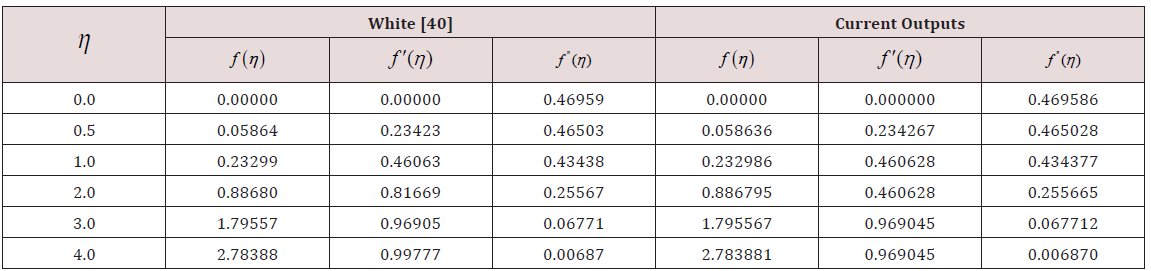
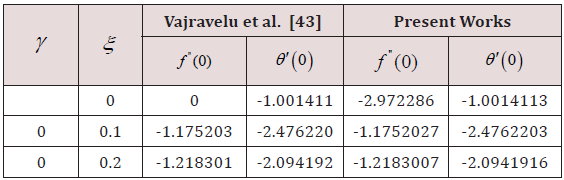
Estimation are carried out by the fourth or fifth order Range Kutta Fehlberg method with shooting technique for different values of parameters. Equations (23) and (24) developed to the boundary conditions (25) have been resolved numerically employing computer software Maple 18. If γ >>1.0 conforms to pure free convection, γ =1.0 correlates to mixed convection and γ <<1.0 corresponds to pure forced convection. Impacts of nanoparticle shapes and solar thermal radiation energy on unsteady Hiemenz water based Cu, Al2O3 and SWCNTs nanofluid flow over a porous wedge sheet are investigated for different values of parameters. In order to justify our method, we have correlated the solutions of f (η ), f ′(η ) and f ′′(η ) for different values of η (Tables 1 & 2) with White [40] whereas f ′′(0) and θ ′(0) for distinct values of ξ (Table 3) with Vajravelu et al. [43] and observed them in desirable acknowledging.

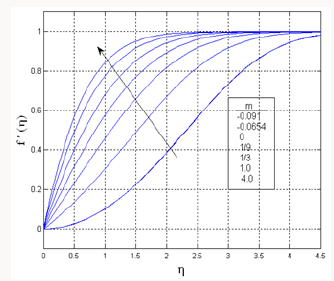
In the nonappearance of energy equation, in order to conform the efficiency of our numerical results, the current work is correlated with the feasible exact result in the literature. The velocity profiles for various values of m are associated with the achievable exact solution of Schlichting [42] (Figure 2). It is noticed that the judgment with the theoretical result of velocity profile is desirable (Figure 3).

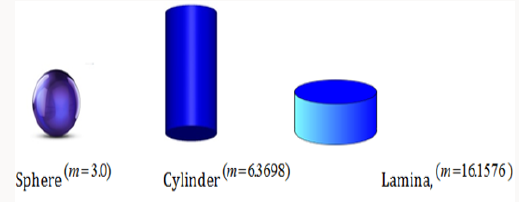
Nanoparticle Shapes

Analysis of Nanoparticle Volume Fraction, with Solar Radiation Energy (Figure 4)

a) Both N = 0.0 and N =1.0 , it is realized that the temperature of all the shape of the nanoparticles (sphere, cylinder and lamina) in the nanofluids (water based Cu, Al2O3 and SWCNTs) increases with increase of nanoparticle volume fraction.

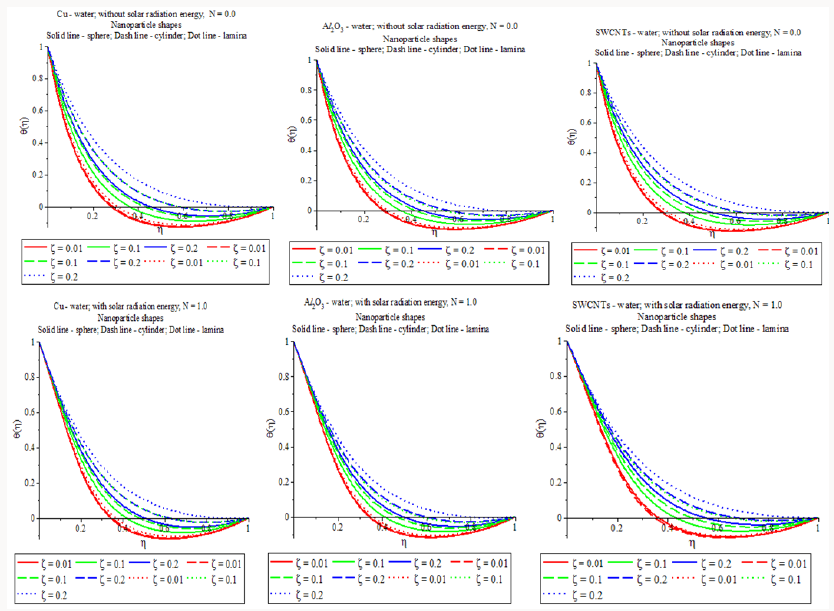
b) In the presence of solar thermal radiation energy N =1.0 , it is amusing to note that the thermal boundary layer width of lamina shape (m =16.1576 ) SWCNTs in SWCNTs-water is stronger as interacted with the other mixtures in the flow region with upturn of nanoparticle volume fraction. This recognize with the physical attitude that when the volume fraction of SWCNTs enhances the thermal conductivity and then the thermal boundary layer thickness developments.

c) In general, the temperature assigning of lamina shape nanoparticles in the water based Cu, Al2O3 and SWCNTs is higher than that of all the other shapes in the flow presidency in the presence of solar radiation energy.

Investigation of Solar Thermal Radiation Energy with Porous Strength (Figure 5)

a) In the presence of porous medium, λ = 5.0 , the temperature distribution of all the shape of the nanoparticles (sphere, cylinder and lamina) in the nano fluids (water based Cu, Al2O3 and SWCNTs) enhances with rise of solar thermal radiation energy.

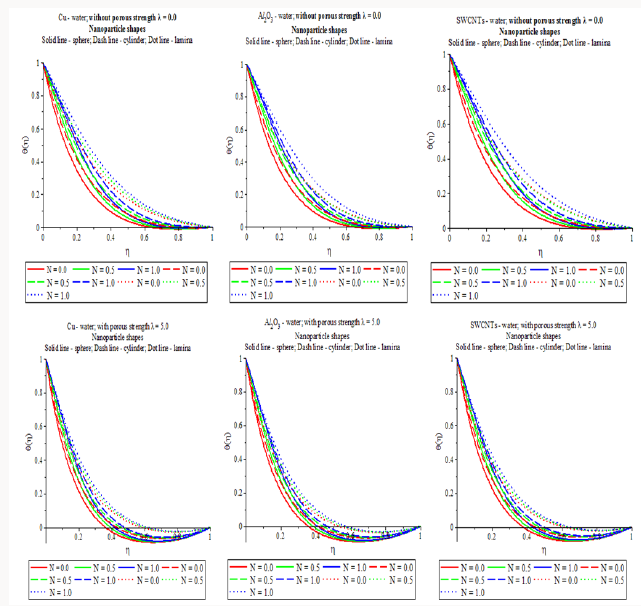
b) Especially, the temperature scattering of lamina shape nanoparticles in the water based Cu, Al2O3 and SWCNTs is more symbolic as compared to the other shapes in the flow tenure with increase of solar radiation energy.

c) The thermal boundary layer girth of lamina shape nanoparticles in the nano fluids water based SWCNTs is more forceful as associated with the other mixtures in the flow system with boost of solar radiation energy.

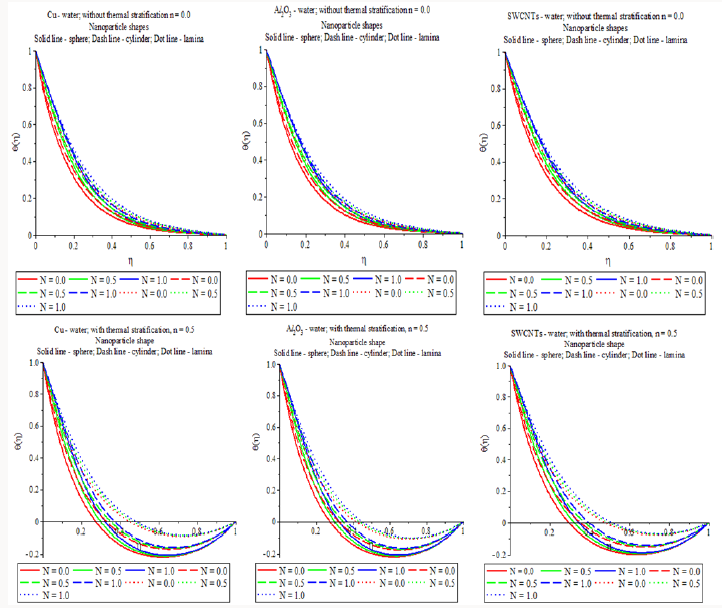
Report of Solar Thermal Radiation Energy with Thermal Stratification (Figure 6)

a) In the presence of n = 0.0 (flow along the wall), it is fascinating to notice that the temperature profiles is bounded within the boundary region while the temperature assigning of vnano fluids (water based Cu, Al2O3 and SWCNTs) for different shapes accelerates with growth of solar radiation energy. All the cases, negative value of the temperature profile develops in the outer boundary region. This is because of the combined effect of thermal stratification and solar thermal radiation energy

b) For heat transfer characteristics mechanism, stimulating solution is the large exaggeration of the temperature field induced for 0.1≤ n <1( n = 0 refers flow at the wall, bottom layer and n =1 refers flow at ambient, upper layer).

c) The temperature distribution of nano fluids (water based Cu, Al2O3 and SWCNTs) for different shapes increases with upturn of solar radiation energy.

d) The temperature transport of laminar shape SWCNTs in SWCNTs-water is more capable as compared to other mixtures in the flow system with upgrade of solar thermal radiation energy.

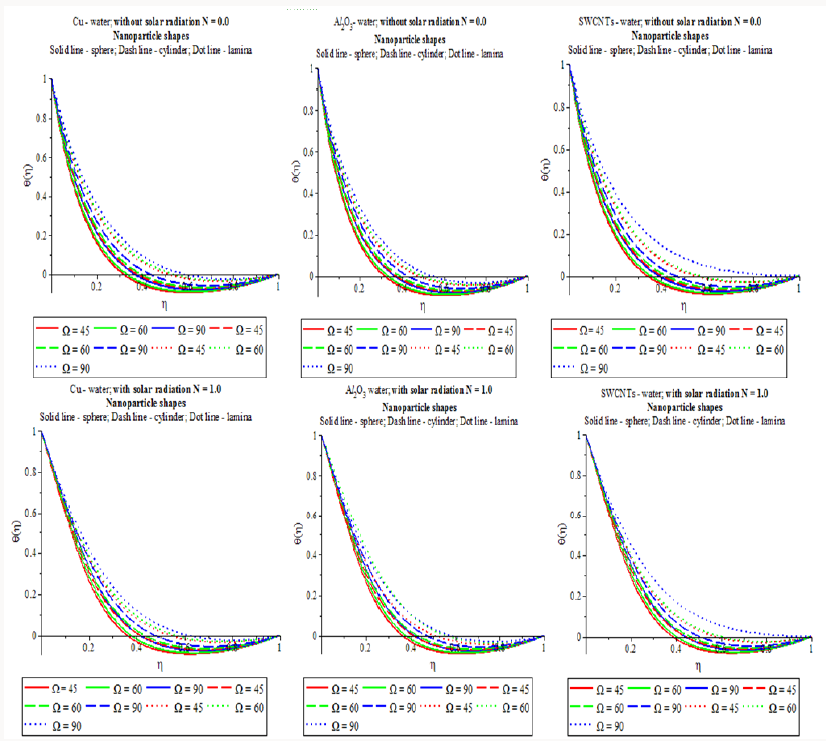
Review of Solar Thermal Radiation Energy with Angle of Inclination (Figure 7)

a) Both N=0.0 and N=1.0, it is seen that the temperature of all the shape of the nanoparticles (sphere, cylinder and lamina) in the nano fluids (water based Cu, Al2O3 and SWCNTs) enhances with increase of nanoparticle volume fraction. As the angle of inclination rises the impact of the buoyancy effects due to thermal diffusion reduces by a aspect of cos Ω/2 . Therefore the dynamic force of the fluid reduces and as a solution the temperature accelerates.

b) In the presence of solar thermal radiation energy N=1.0, it is amusing to note that the thermal boundary layer thickness of lamina shape (m =16.1576 ) SWCNTs in SWCNTs-water plays a dominant role as compared with other mixture in the flow scheme with rise of angle of inclination.

c) The temperature distribution of lamina shape nanoparticles in the water based Cu, Al2O3 and SWCNTs is more significant as compared to other mixtures in the flow regime with increase of angle of inclination. This effort of passing the absorbing nano fluid through an absorbing porous wedge medium is regarded to raise solar collection by absolute absorption in which heat falls are decreased as an output of plate temperatures.

Survey of Rate of Heat Transfer (Table 4)

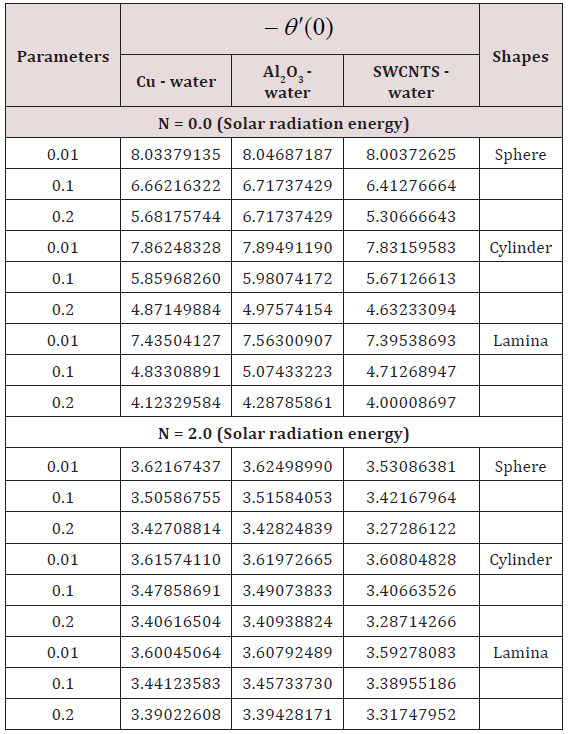
Impact of Nanoparticle Volume Fraction without Solar Radiation Energy:

a) The rate of heat transfer of sphere shape alumina nanoparticles in the presence of Al2O3 -water is stronger (ζ = 0.01;−θ ′(0) = 8.04687187 ) than that of all the other nanoparticle shapes in the presence of various mixtures in the flow regime.

b) The rate of heat transfer of lamina shape SWCNTs nanoparticles in the presence of SWCNTs-water is lower (ζ = 0.2;−θ ′(0) = 4.00008697 ) as compared all the other mixtures in the flow regime.

Performance of Nanoparticle Volume Fraction with Solar Radiation Energy:

a) The rate of heat transfer of sphere shape alumina nanoparticles in the presence of Al2O3-water is stronger (ζ = 0.01;−θ ′(0) = 3.62498990 ) as correlated with the other mixtures in the flow regime.

b) The rate of heat transfer of sphere shape SWCNTs nanoparticles in the presence of SWCNTs-water is lower (ζ = 0.2;−θ ′(0) = 3.27286122 ) as associated with the other mixtures in the flow regime which means that the SWCNTs - water will be important in the cooling and heating processes [44-50].

Conclusion

Subject of nanoparticle shapes (sphere, cylinder and lamina) on Hiemenz nano fluids (water, ethylene glycol and engine oil based Cu, Al₂O₃ and SWCNTs) flow over a porous wedge in design of solar radiation energy has been analyzed in this work. Reorganization of heat transfer rate and temperature within the nano fluids with distinct nanoparticle shapes are predicted in terms of Figures and Tables and the issues of the analysis are placed as follows:

a) The temperature empowering of lamina shape nanoparticles in the water based Cu, Al₂O₃ and SWCNTs is more advanced than that of all the other shapes in the flow system with increase of solar radiation energy in the presence of all the other effects in the flow regime.

b) The lamina shape SWCNTs in SWCNTs - water plays symbolic possessions on temperature distribution with raise of solar thermal radiation energy as compared to all the other shapes in the flow region which means that the SWCNTs - water will be important in the heating processes.

c) The rate of heat transfer of sphere shape alumina nanoparticles in the presence of Al₂O₃-water is stronger as correlated with the other mixtures in the flow scheme.

d) The rate of heat transfer of sphere shape SWCNTs nanoparticles in the presence of SWCNTs-water is not more significant as associated with the other mixtures in the flow regime.

It is registered that the lamina shape SWCNTs in the existence of water based SWCNTs is researched in this work can be gainful in the solar radiation energy systems. Resultantly, the lamina shape SWCNTs in the SWCNTs-water is a more affirmation in terms of complementing the heat transfer reinforcement of the Hiemenz flow system over a porous wedge surface.

Acknowledgement

The authors also would like to thank Universiti Tun Hussein Onn Malaysia and Ministry of Higher Education, Malaysia for their financial support, (IGSP/U246/2014-2016).

Nomenclature

C_T Temperature ratio

C_P Specific heat at constant pressure,

g Acceleration due to gravity,

k₁ Rate of chemical reaction,

k* Absorption coefficient

K Permeability of the porous medium

k_f Thermal conductivity of the base fluid

k_s Thermal conductivity of the nanoparticle

k_fn Effective thermal conductivity of the nanofluid

n Thermal stratification parameter

q′′_rad Incident radiation flux of intensity

T Temperature of the fluid,

T_w Temperature of the wall,

T_∞ Temperature of the fluid far away from the wall,

u,v Velocity components in x and y direction,

U(x) Flow velocity of the fluid away from the wedge,

V₀ Velocity of suction / injection,

Greek symbols

α_fn

β_fThermal expansion coefficients of the base fluid

β_s Thermal expansion coefficients of the nanoparticle

ρ_f Density of the base fluid

ρ_s Density of the nanoparticle

ρ_fn Effective density of the nanofluid

(ρ c_p)f_n Heat capacitance of the nanofluid

σ₁ Stefan - Boltzman constant

κ Thermal conductivity of the fluid

μ_f Dynamic viscosity of the base fluid

μ_fn Effective dynamic viscosity of the nanofluid,

δ Time-dependent length scale

Ω Angle of inclination of the wedge

ξ Dimensionless distance along the wedge

ζ Nanoparticle volume fraction

References

1. Sharma, VV Tyagi, CR Chen, D Buddhi (2009) Review on thermal energy storage with phase change materials and applications. Renew. Sust Energy Rev 13(2): 318-345.
2. AJ Hunt (1978) Small particle heat exchangers, Lawrence Berkeley Laboratory report no. LBL-7841. J Renew Sust Energy
3. S Choi (1995) Enhancing thermal conductivity of fluids with nanoparticle. In: DA Siginer, HP Wang (Eds.); Developments and Applications of Non- Newtonian Flows, ASME MD 231: 99-105.
4. J Buongiorno, W Hu (2005) Nanofluid coolants for advanced nuclear power plants, Paper no. 5705 Proceedings of ICAPP ‘05 Seoul p. 15-19.
5. J Buongiorno (2006) Convective transport in nanofluids, ASME J Heat Transf 128: 240-250.
6. P Cheng, W Minkowycz (1977) Free convection about a vertical flat plate embedded in a porous medium with application to heat transfer from a dike. J Geophys Res 82: 2040-2044.
7. A Mufuoglu, E Bilen (2008) Heat transfer in inclined rectangular receivers for concentrated solar radiation. Int Commun Heat Mass Transfer 35(5): 551-556.
8. R Kandasamy, I Muhaimin, AB Khamis, RB Roslan (2013) Unsteady Heimenz flow of Cu-nanofluid over a porous wedge in the presence of thermal stratification due to solar energy radiation: Lie group transformation. Int J Therm Sci 65: 196-205.
9. K Das, PR Duari, PK Kundu (2014) Solar radiation effect on Cu-water nanofluid flow over a stretching sheet with surface slip and temperature jump. Arab J Sci Eng 39(12): 9015-9023.
10. N Anbuchezhian, K Srinivasan, K Chandrasekaran, R Kandasamy (2013) Magneto hydrodynamic effects on natural convection flow of a nanofluid in the presence of heat source due to solar energy. Meccanica 48(2): 307-321.
11. T Yousefi, F Veysi, E Shojaeizadeh, S Zinadini (2012) An experimental investigation on the effect of Al2O3–H2O nanofluid on the efficiency of flat-plate solar collectors. Renewable Energy 39(1): 293-298.
12. T Yousefi, E Shojaeizadeh, F Veysi, S Zinadini (2012) An experimental investigation on the effect of pH variation of MWCNT-H2O nanofluid on the efficiency of a flat-plate solar collector. Sol Energy 86(2): 771-779.
13. Y Kameya, K Hanamura (2011) Enhancement of solar radiation absorption using nanoparticle suspension. Sol Energy 85(2): 299-307.
14. A Lenert, EN Wang (2012) Optimization of nanofluid volumetric receivers for solar thermal energy conversion. Sol Energy 86(1): 253- 265.
15. Q He, S Wang, S Zeng, Z Zheng (2013) Experimental investigation on photothermal properties of nanofluids for direct absorption solar thermal energy systems. Energy Convers Manage73: 150-157.
16. T Sokhansefat, AB Kasaeian, k_fowsary (2014) Heat transfer enhancement in parabolic trough collector tube using Al2O3/synthetic oil nanofluid. Renew Sustain Energy Rev 33: 636-644.
17. AN Al-Shamani, MH Yazdi, MA Alghoul, AM Abed, MH Ruslan, et al. (2014) Nanofluids for improved efficiency in cooling solar collectors - A review. Renew Sustain Energy Rev 38: 348-367.
18. A Kasaeian, AT Eshghi, M Sameti (2015) A review on the applications of nanofluids in solar energy systems. Renew Sustain Energy Rev 43: 584-598.
19. P Mohammad Zadeh, T Sokhansefat, AB Kasaeian, k_fowsary, A Akbarzadeh (2015) Hybrid optimization algorithm for thermal analysis in a solar parabolic trough collector based on nanofluid. Energy 82: 850- 864.
20. M Sardarabadi, M Passandideh-Fard, S Zeinali Heris (2014) Experimental investigation of the effects of silica/water nanofluid on PV/T [Photovoltaic thermal units]. Energy 66: 264-272.
21. P Chandrasekaran, M Cheralathan, V Kumaresan, R Velraj (2014) Enhanced heat transfer characteristics of water based copper oxide nanofluid PCM (phase change material) in a spherical capsule during solidification for energy efficient cool thermal storage system. Energy 72: 636-642.
22. AM Hussein, KV Sharma, RA Bakar, K Kadirgama (2014) A review of forced convection heat transfer enhancement and hydrodynamic characteristics of a nanofluid. Renew Sustain Energy Rev 29: 734-743.
23. F Javadi, R Saidur, M Kamalisarvestani (2013) Investigating performance improvement of solar collectors by using nanofluids. Renew Sustain Energy Rev 28: 232-245.
24. L Syam, MK Sundar Singh (2013) Convective heat transfer and friction factor correlations of nanofluid in a tube and with inserts: A review. Renew Sustain Energy Rev 20: 23-35.
25. Ali J Chamkha, ARA Khaled (2001) Similarity solutions for hydro magnetic simultaneous heat and mass transfer. Heat Mass Transf 37(2- 3): 117-125.
26. MA Seddeek, AA Darwish, MS Abdelmeguid (2007) Effects of chemical reaction and variable viscosity on hydromagnetic mixed convection heat and mass transfer for Heimenz flow through porous media with radiation. Commun Nonlinear Sci Numer Simul 12(2): 195-213.
27. R Tsai, JS Huang (2009) Heat and mass transfer for Soret and Dufour’s effects on Heimenz flow through porous medium onto a stretching surface. Int J Heat Mass Transf 52(9-10): 2399-2406.
28. Gamal Abdel Rahman (2010) Thermal-diffusion and MHD for Soret and Dufour’s effects on Heimenz flow and mass transfer of fluid flow through porous medium onto a stretching surface. Physica B 405(11): 2560-2569.
29. K Hiemenz (1911) Die Grenzschicht an einem in den gleichfoÈrmigen FluÈssigkeitsstrom eingetauchten geraden Kreiszylinder. Dingl Poltech J 326: 321-410.
30. KA Yih (1998) The effect of uniform suction/blowing on heat transfer of Magnetohydrodynamic Hiemenz flow through porous media. Acta Mech 130(3-4): 147-158.
31. AA Avramenko, SG Kobzar, IV Shevchuk, AV Kuznetsov, LT Iwanisov (2001) Symmetry of turbulent boundary layer flows: Investigation of different Eddy viscosity models. Acta Mech 151(1-2): 1-14.
32. EV Timofeeva, JL Routbort, D Singh (2009) Particle shape effects on thermo physical properties of alumina nanofluids. Journal of Applied Physics 106(1): 014304.
33. SUS Choi (2009) Nanofluids: From vision to reality through research. J Heat Transf 131: 1-9.
34. EM Sparrow, RD Cess (1978) Radiation heat transfer Hemisphere. Washington, USA.
35. A Raptis (1998) Radiation and free convection flow through a porous medium. Int Comm Heat Mass Transfer 25: 289-295.
36. MQ Brewster (1972) Thermal Radiative Transfer Properties, John Wiley & Sons, New York, USA.
37. MA Sattar (1994) Unsteady hydromagnetic free convection flow with Hall current, mass transfer and variable suction through a porous medium near an infinite vertical porous plate with constant heat flux, International Journal of Energy Research 18(9): 771-777.
38. SM Aminossadati, B Ghasemi (2009) Natural convection cooling of a localized heat source at the bottom of a nanofluid-filled enclosure. J Mech Fluids 28(5): 630-640
39. JCA Maxwell (1891) A Treatise on Electricity and Magnetism, 2 unabridged (3rd edn); Clarendon Press, Oxford, UK.
40. FM White (2006) Viscous Fluid Flows (3rd edn.); McGraw-Hill, New York, USA.
41. NG Kafoussias, ND Nanousis (1997) Magneto hydrodynamic laminar boundary layer flow over a wedge with suction or injection. Canadian Journal of Physic 75(10): 733-781.
42. H Schlichting (1979) Boundary Layer Theory. McGraw Hill Inc, New York, USA.
43. K Vajravelu, KV Prasad, Jinho Lee, Changhoon Lee, I Pop et al. (2011) Convective heat transfer in the flow of viscous Ag-Water and Cu-water nanofluids over a stretching surface. International Journal of Thermal Sciences 50(5): 843-851.
44. NG Kafoussias, ND Nanousis (1997) Magneto hydrodynamic laminar boundary layer flow over a wedge with suction or injection. Can J Phys 75(10): 733-781.
45. Anjali Devi, R Kandasamy (2001) Effects of heat and mass transfer on MHD laminar boundary layer flow over a wedge with suction or injection. J Energy Heat Mass Transf 23: 167-178.
46. T Watanabe (1990) Thermal boundary layer over a wedge with uniform suction or injection in forced flow. Acta Mech 83(4): 119-126.
47. MA Hossian (1992) Viscous and Joule heating effects on MHD free convection flow with variable plate temperature. Int J Heat Mass Transf 35(12): 3485-3492.
48. Kuo Bor Lih (2005) Heat transfer analysis for the Falkner-Skan wedge flow by the differential transformation method. Int J Heat Mass Transf 48(24): 5036-5042.
49. WT Cheng, HT Lin (2002) Non-similarity solution and correlation of transient heat transfer in laminar boundary layer flow over a wedge. Int J Eng Sci 40(5): 531-540.
50. PVSN Murthy, S Mukherjee, D Srinivasacharya, PVSSSR Krishna (2004) Combined radiation and mixed convection from a vertical wall with suction / injection in a non-Darcy porous medium. Acta Mechanica 168(4): 145-156.