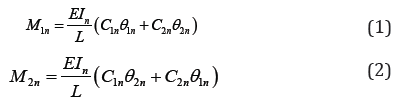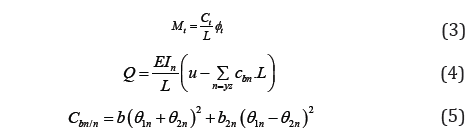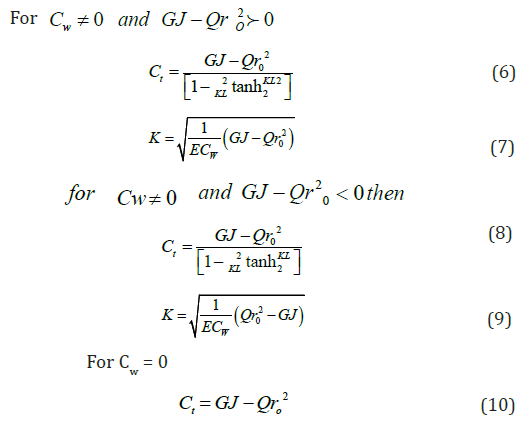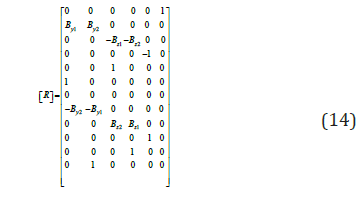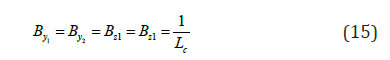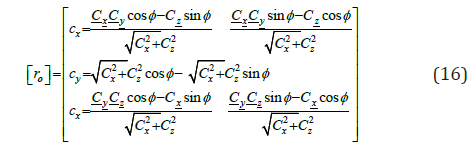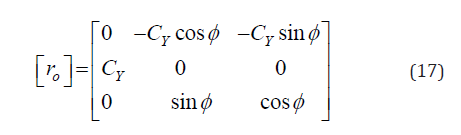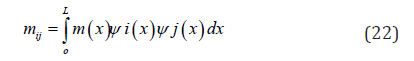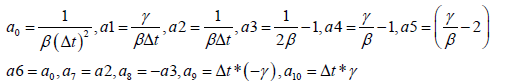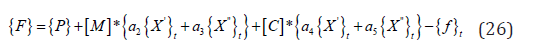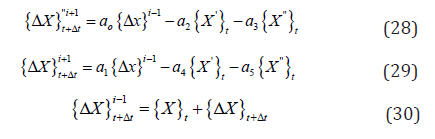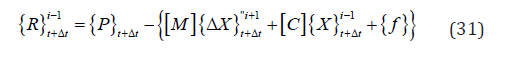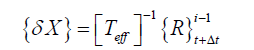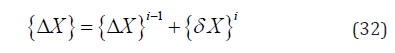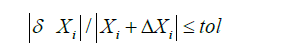Nonlinear Analysis of Space Structures under Dynamic Loads Volume 2 - Issue 3

Qasim M Shakir*

• University of Kufa, Iraq

Received: May 18, 2018;   Published: June 11, 2018

Corresponding author: Qasim M Shakir, University of Kufa, Iraq

DOI: 10.32474/TCEIA.2018.02.000140

Abstract PDF

---

Abstract

A theoretical analysis is presented for estimating the in-space large displacement elastic stability behavior of structures subjected to either proportional or non-proportional dynamic loads. The analysis adopts the beam-column approach, which models the structure’s members as beam-column elements. The formulation of the beam-column element is based on the Eulerian approach allowing for the influence of the axial force on the bending and the torsion stiffness. Also, change in member chord length due to the axial deformation and flexural bowing are taken into account. Newmark- β method is used as a time integration technique to plot the time-deformation curves. Damping effect is expressed using Raleigh damping matrix. Several examples have been solved to insure the accuracy of the present analysis.

Introduction

A dynamic load may cause instability of a structure, even if the structure remains stable under a static load of the same magnitude as the dynamic load .Such phenomenon may occur within the elastic range. So, the maximum deformation response abruptly increases at some point with respect to the magnitude of loading. When this kind of instability problem to be solved ,geometrical non-linearity must be considered in the dynamic analysis as that in static instability analysis. To days, studies conducted on dynamic analysis of frames with geometric non-linearity are mainly concerned with plane frames. Such studies dealing with three dimensional frames are seldom found in the literature. The objective of this paper is to extend the large deformation static analysis of space structures presented previously by Oran [1] and then by kassimali and abbsania [2] to deal with the time dependent loading. Members are assumed to be prismatic connected by frictionless hinges for trusses and rigid joints for frames.

Basic Member Force Deformation Relations

The basic member force-deformation relations consistent with the conventional beam column theory [1] Figure 1 are:

Both stability and bowing are dependent on the axial force parameter (qn) and their explicit transcendental and series expressions are given by Oran [3,1] and kassimali and abbsania [2].

The torsional factor (Ct) in equation [4] considers the influence of axial force on member torsional stiffness [1]

Member End Effects

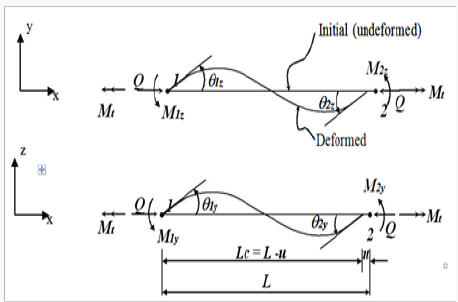
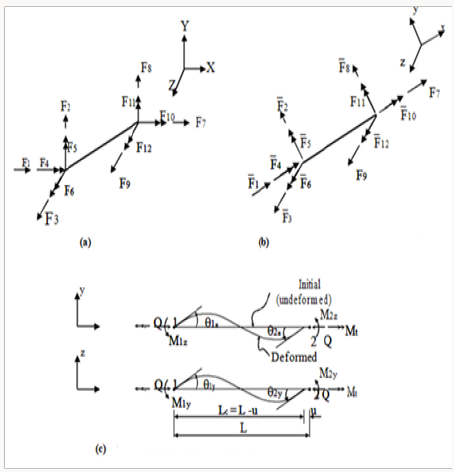
Consider an arbitrary prismatic member of a space frame, and let {F} and {F’} denote member end forces in the global and local coordinates respectively (Figures 2a & 2b), the relationship between {F} and {F’} can be written as:

{F}=[R]{¯F} (11)

[R]: is the (12x12) orthogonal matrix [5] and defined as:

[r]: is the (3x3) member orientation matrix, refers to the deformed configuration of the member. This matrix refers to the deformed configuration and must be updated according to the N-R type technique [6]. Similarly the member forces {F}are related to the forces {S} associated with the relative member deformations (Figures 2b & 2c) by:

{F}=[B]{S} (13)

[B]: is the instantaneous static matrix defined as:

In which

Member orientation matrix

Initial member orientation matrix [r₀]

It must be used for the first increment and for the first iteration only. This matrix can be derived by taking in consideration that the transformation from the local to the global coordinates to take place by rotating the member through the angles (β,  and ) about the Z-, Y- and X-axis, (Figures 3a & 3b).The final form of this matrix is [5]:

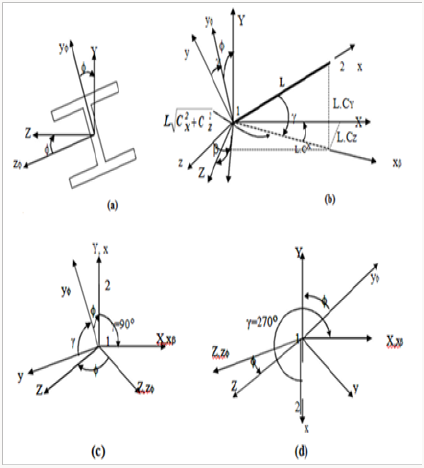
When the member is vertical, the initial member orientation matrix [r₀] will be :

CY = 1 for γ=900 and CY =-1 for γ=2700

Current Member Orientation Matrix

Three alternate methods are available in the literature that are used to determine the current member orientation matrix for the deformed configuration. Two of these are presented by Oran [1] and the third one was presented by Kassimali and Abbasania [2]. One of the procedures of Oran was utilized in the present analysis. This method is based on the variation of the principal directions from one section to another, then the incremental joint orientation matrix is calculated in each increment, and the total joint orientation matrix is updated for the next increment. The current member orientation matrix, then, is obtained by averaging the orientation of the two end sections of the member [1]. Thus, the current member orientation matrix can be expressed as:

[r]=1/2{[D⁽¹⁾]+[D⁽²⁾]} (18)

Where [D(1)],[D(2)]: are the current section orientation matrices of the two ends of the member.

Member Tangent Stiffness Matrix

The incremental relationship between the end forces and the end displacements {ΔV} in the global coordinates can be written as:

{ΔF} = [T ]{ΔV} (19)

And [T] is the member tangent stiffness matrix in global coordinates which can be written [6][11] as:

[T]=[R][B][t][B]+^TΣ _K=I⁶S_{K[g^{-(-k)][RT] (20)}}

Where [T] is the member tangent stiffness matrix inb eulerian coordinates and it is gien axlicity with [g(k)] in Appendix I.

Dynamic Analysis

The dynamic equation of motion [7,8] for nonlinear systems can be written as

[M]{X¢¢}+[C]{X¢}+[T]{X} = [F ( t )] (21)

The consistent mass method has been adopted in the present study. In this method, mass coefficients corresponding to the nodal coordinates can be evaluated depending on the principle of virtual work. Accordingly, the mass coefficients can be given in a general form as:

Damping matrix has been represented using the so-called Raylieh type of damping which may be expressed as:

[C] =α₁ [M] + α₂[T] (23)

The Computational Technique

The nonlinear dynamic response of structures is investigated in this work using the step -by -step numerical integration procedure with a Newton type of iteration performed within each time step to satisfy the equation of motion .The Newmark -β method with β=1/4 and γ=1/2 is used

Assuming that the displacement, velocity and acceleration vectors are known at time to=0

Then, the general procedure of analysis is as follows [9,10]

a) Calculate the following constants

b) form the matrices [T],[M] and [c] for each member ,then, form the overall matrices by the assemblage of the element stiffness matrices

c) From the effective stiffness matrix, initially assuming linear behaviour

[T_eff]=a₁[M]+a₂[C]+[T] (24)

[C] =b₁ [M]+b₁[T] (25)

d) From the effective load vector

e) Solve for the increment displacements (for time t + Δt )

f) iterate for dynamic equilibrium

a. i=i+1

b. evaluate the ( i-1 )th approximation of acceleration, velocity and displacement vectors

c. evaluate the (i-1)th unbalanced joint forces

d. compute the correction of the displacement increment {ΔX}

e. evaluate the corrected displacement vector

f. check for convergence

g. if “No” ,go to 6.a else return to step 3 to proceed to the next time step

Applications

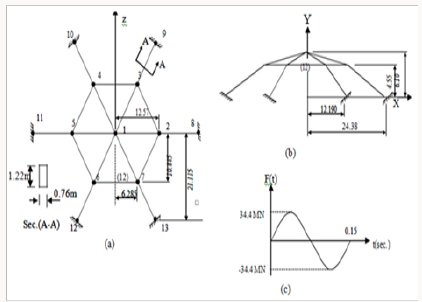
Framed Dome under Harmonic Loading

The response due to a harmonically varying vertical load at the crown of the dome shown in Figure 4 has been studied by Remesth [11] using the finite element approach with two elements per member . Newmark-method with ( β=1/4 and γ=1/2 ) has been used. The peak value of the concentrated load is chosen to be (34.4MN) with time step size of (0.0025sec) and natural frequency of the applied load is taken to be (0.15sec).Damping is included in the analysis and it is determined from a model damping ratio (5%) for the mode with the longest natural period initially equal to (0.175sec). 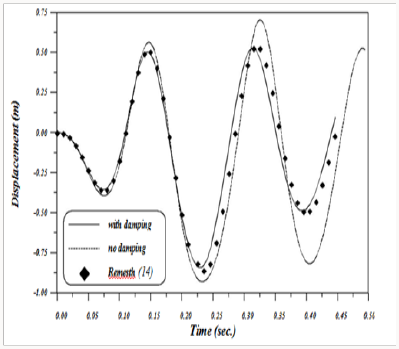This example is analyzed in the present work with and without damping using Newmark method with the same load properties, each member is modeled with one element and the vertical response of the loaded joint for both studies is illustrated in Figure 5. 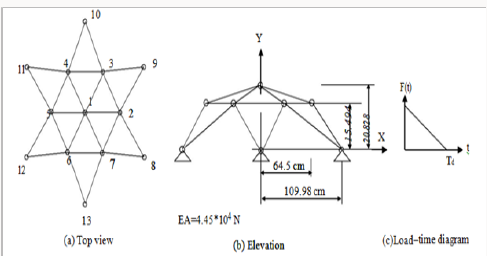It is clear that a good agreement may be obtained using the present analysis including damping effects.

Geodesic Dome under Triangular Load

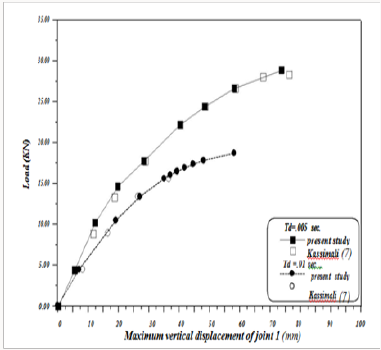
The geodesic dome shown in Figure 6 is to be analyzed under triangular dynamic load applied at the central point [6] Kassimali and Bedhendi [12] analyzed this structure using a stiffness method based on an Eulerian formulation accounting for arbitrarily large displacements. Two time durations (Td=0.005sec, Td=0.01 sec) were used. It was found that for short impulse duration, the critical load decreases steadily as duration increases and it approaches that of the static load case for long time durations. 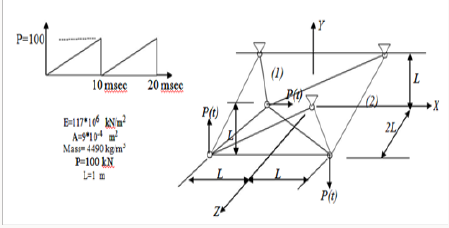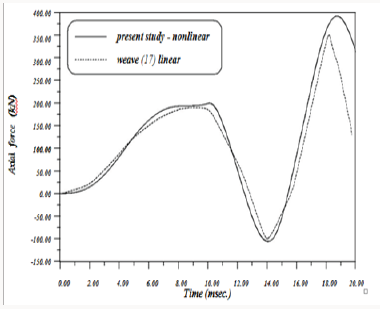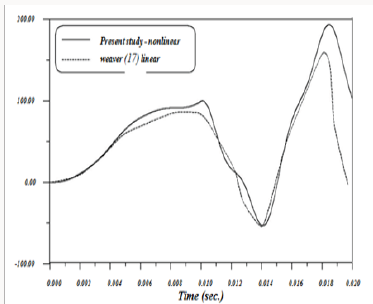The problem is solved in this study under the same loading conditions and the results are shown in Figure 7 which indicates the efficiency of the computer program developed in the present study to predict the large displacement behaviour of space frames under dynamic loads.

Space Truss with Nine Prismatic Elements

The space truss shown in Figure 8 has been analyzed by Weaver [5] using linear analysis .The same structure is considered here to show the importance of studying large deformations for such structures under dynamic loads. The variation of axial force with time for members [6,13] for both studies are shown in Figure 9 & 10. It is obvious that at time(t=19 msec),the linear analysis underestimates the axial forces for the two members by (15%) and (30%) respectively [14-17].

Conclusion

The present work shows the importance of considering the large deformations behaviour in the analysis of space structure under dynamic loading within elastic range. The beam column which have been utilized previously for the analysis of plane structures under static and dynamic loads and also for space structures under static loading is extended in this work to deal with the analysis of space structures under dynamic loading.

Although of its simplicity, Rayleigh model may be adopted to represent the damping effects. Also it is found that the method of updating the member orientation matrix by averaging the end section orientation matrices is adequate enough to be adopted in the analysis of space structures subjected to time dependent loading (Appendixs 2 & 3).

References

1. Avsek, T (2014) Study of Rainfall –Runoff Simulation using HEC-HMS model: A few case studies in West Bengal; unpublished dissertation submitted to the School of Water Resources. Engineering Affiliated to the Jadavpur University Kolkata India pp. 1-11.
2. Levi DB, Julie EK, Olsen JR, Pulwarty RS, Raff DA, et al. (2009) Climate Change and Water Resources Management: A Federal Perspective. circular 1331 pp.1-72.
3. Olusegun A, Mahe G, Claudine D, Elbaz Poulicher F, Rouche N, et al. (2012) Rainfall-Runoff Simulation in part of Lower Niger Basin. Journal of Environmental Science and Engineering 1: 812-819.
4. Oyebode EO, Adekalu KO, Fashoto SG (2010) Development of Rainfall- Runoff Forecast Model. International Journal of Engineering and Mathematical Intelligence 1(1-3): 56-66.
5. Raes D, Willens P, Gbaguidi (2006) Rainbow – A software package for analyzing data and testing the homogeneity of historical data sets 1: 1-15.
6. Ralf M, Gunter B, Juraj P (2006) Regionalization method in rainfall-runoff modelling using catchment samples, large sample basin experiment for hydrological model parameterization. Results of the Model parameter Experiment – MOPEX IAHS 307: 117-125.
7. Saleh A (2012) Runoff Modelling by HEC-HMS Model (case study: Kan Watershed, Iran). International Journal of Agriculture and crop science 4(23): 1807-1811.
8. Supe MS, Taley SM, Kale MU (2015) Rainfall-Runoff Modelling using HEC-HMS for Wan River Basin. International Journal of Research in Engineering, Science and Technology 1(8): 21-29.
9. Waymire E, Gupta VK (1981) The Mathematical Structure of Rainfall Representations. Water Resources Research Journal 17(5): 1261-1294.